Addition and Subtraction With Fractions
Addition and subtraction with fractions works exactly the same way as it does with whole numbers, with one important distinction: the denominators of the fractions you add together have to be the same. For example:
1⁄4 + 2⁄4 = 3⁄4
So, what do you do if you need to add two fractions with different denominators? Simple: you need to find a common denominator for the two fractions. For example:
If you want to solve the equation "2⁄3 - 1⁄2 = x," you need to find the common denominator of 2⁄3 and 1⁄2. Remember, fractions are parts of a whole. Think of these fractions as though they were pie charts.
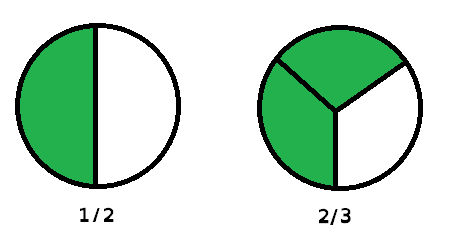
The denominator is the number of "slices" in the pie chart. In order to increase the denominator, you can add more slices, but they all have to be of equal size. Mathematically, the way we do this is to multiply the top and bottom of each fraction by the other's denominator, like this:
2⁄3 * 2⁄2 = 4⁄6
1⁄2 * 3⁄3 = 3⁄6
After this is done, you can see the pie charts look the same, but with more slices.
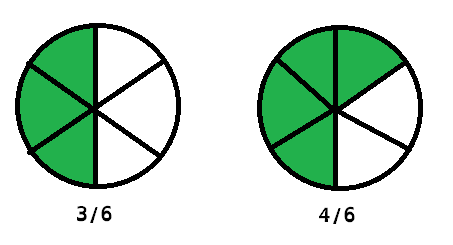
Now, you can solve your equation the same way as you did the first one.
4⁄6 - 3⁄6 = 1⁄6
This strategy works with all addition and subtraction problems involving fractions.